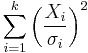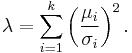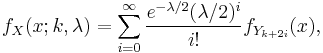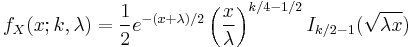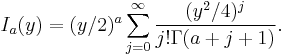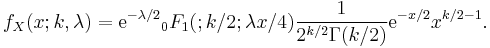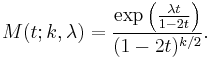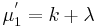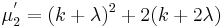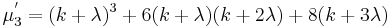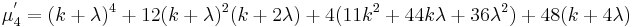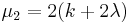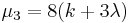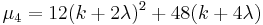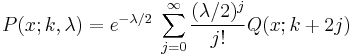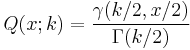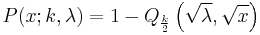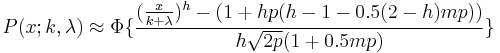Noncentral chi-squared distribution
| Probability density function |
|
| Cumulative distribution function |
|
| Parameters | 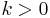 degrees of freedom degrees of freedom
|
|---|---|
| Support | 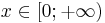 |
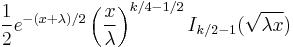 |
|
| CDF | 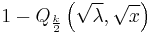 with Marcum Q-function with Marcum Q-function 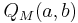 |
| Mean | 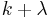 |
| Variance | 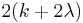 |
| Skewness | 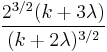 |
| Ex. kurtosis | 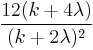 |
| MGF | 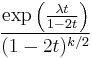 for for  |
| CF | 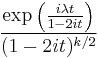 |
In probability theory and statistics, the noncentral chi-squared or noncentral 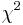 distribution is a generalization of the chi-squared distribution. This distribution often arises in the power analysis of statistical tests in which the null distribution is (perhaps asymptotically) a chi-squared distribution; important examples of such tests are the likelihood ratio tests.
distribution is a generalization of the chi-squared distribution. This distribution often arises in the power analysis of statistical tests in which the null distribution is (perhaps asymptotically) a chi-squared distribution; important examples of such tests are the likelihood ratio tests.
Contents |
Background
Let 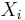 be k independent, normally distributed random variables with means
be k independent, normally distributed random variables with means 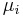 and variances
and variances 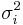 . Then the random variable
. Then the random variable
is distributed according to the noncentral chi-squared distribution. It has two parameters:  which specifies the number of degrees of freedom (i.e. the number of
which specifies the number of degrees of freedom (i.e. the number of 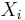 ), and
), and  which is related to the mean of the random variables
which is related to the mean of the random variables 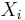 by:
by:
 is sometime called the noncentrality parameter. Note that some references define
is sometime called the noncentrality parameter. Note that some references define  in other ways, such as half of the above sum, or its square root.
in other ways, such as half of the above sum, or its square root.
This distribution arises in multivariate statistics as a derivative of the multivariate normal distribution. While the central chi-squared distribution is the squared norm of a random vector with 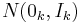 distribution (i.e., the squared distance from the origin of a point taken at random from that distribution), the non-central
distribution (i.e., the squared distance from the origin of a point taken at random from that distribution), the non-central 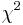 is the squared norm of a random vector with
is the squared norm of a random vector with 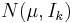 distribution. Here
distribution. Here 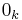 is a zero vector of length k,
is a zero vector of length k, 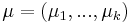 and
and 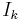 is the identity matrix of size k.
is the identity matrix of size k.
Properties
Probability density function
The probability density function is given by
where 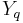 is distributed as chi-squared with
is distributed as chi-squared with  degrees of freedom.
degrees of freedom.
From this representation, the noncentral chi-squared distribution is seen to be a Poisson-weighted mixture of central chi-squared distributions. Suppose that a random variable J has a Poisson distribution with mean 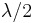 , and the conditional distribution of Z given
, and the conditional distribution of Z given 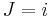 is chi-squared with k+2i degrees of freedom. Then the unconditional distribution of Z is non-central chi-squared with k degrees of freedom, and non-centrality parameter
is chi-squared with k+2i degrees of freedom. Then the unconditional distribution of Z is non-central chi-squared with k degrees of freedom, and non-centrality parameter  .
.
Alternatively, the pdf can be written as
where 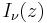 is a modified Bessel function of the first kind given by
is a modified Bessel function of the first kind given by
Using the relation between Bessel functions and hypergeometric functions, the pdf can also be written as:[1]
Siegel (1979) discusses the case k=0 specifically (zero degrees of freedom), in which case the distribution has a discrete component at zero.
Moment generating function
The moment generating function is given by
The first few raw moments are:
The first few central moments are:
The nth cumulant is
Hence
Cumulative distribution function
Again using the relation between the central and noncentral chi-squared distributions, the cumulative distribution function (cdf) can be written as
where 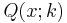 is the cumulative distribution function of the central chi-squared distribution with k degrees of freedom which is given by
is the cumulative distribution function of the central chi-squared distribution with k degrees of freedom which is given by
- and where
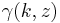 is the lower incomplete Gamma function.
is the lower incomplete Gamma function.
The Marcum Q-function 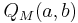 can also be used to represent the cdf.[2]
can also be used to represent the cdf.[2]
Approximation
Sankaran [3] discusses a number of closed form approximations for the cumulative distribution function. In an earlier paper,[4] he derived and states the following approximation:
where
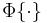 denotes the cumulative distribution function of the standard normal distribution;
denotes the cumulative distribution function of the standard normal distribution;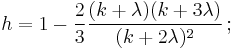
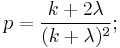
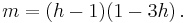
This and other approximations are discussed in a later text book.[5]
To approximate the Chi-squared distribution, the non-centrality parameter, 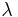 , is set to zero.
, is set to zero.
For a given probability, the formula is easily inverted to provide the corresponding approximation for 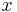 .
.
Derivation of the pdf
The derivation of the probability density function is most easily done by performing the following steps:
- First, assume without loss of generality that
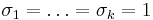 . Then the joint distribution of
. Then the joint distribution of  is spherically symmetric, up to a location shift.
is spherically symmetric, up to a location shift. - The spherical symmetry then implies that the distribution of
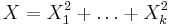 depends on the means only through the squared length,
depends on the means only through the squared length, 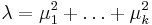 . Without loss of generality, we can therefore take
. Without loss of generality, we can therefore take 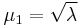 and
and 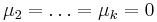 .
. - Now derive the density of
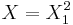 (i.e. k=1 case). Simple transformation of random variables shows that :
(i.e. k=1 case). Simple transformation of random variables shows that :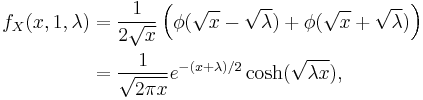
where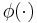 is the standard normal density.
is the standard normal density. - Expand the cosh term in a Taylor series. This gives the Poisson-weighted mixture representation of the density, still for k=1. The indices on the chi-squared random variables in the series above are 1+2i in this case.
- Finally, for the general case. We've assumed, without loss of generality, that
 are standard normal, and so
are standard normal, and so  has a central chi-squared distribution with (k-1) degrees of freedom, independent of
has a central chi-squared distribution with (k-1) degrees of freedom, independent of 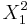 . Using the poisson-weighted mixture representation for
. Using the poisson-weighted mixture representation for 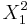 , and the fact that the sum of chi-squared random variables is also chi-squared, completes the result. The indices in the series are (1+2i)+(k-1) = k+2i as required.
, and the fact that the sum of chi-squared random variables is also chi-squared, completes the result. The indices in the series are (1+2i)+(k-1) = k+2i as required.
Related distributions
- If
 is chi-squared distributed
is chi-squared distributed 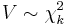 then
then  is also non-central chi-squared distributed:
is also non-central chi-squared distributed: 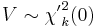
- If
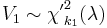 and
and 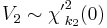 and
and 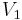 is independent of
is independent of 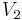 then a noncentral F-distributed variable is developed as
then a noncentral F-distributed variable is developed as 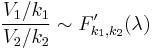
- If
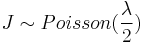 , then
, then 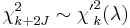
- Normal approximation[6]: if
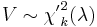 , then
, then 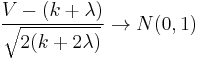 in distribution as either
in distribution as either 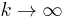 or
or 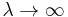 .
.
Transformations
Sankaran (1963) discusses the transformations of the form ![z=[(X-b)/(k%2B\lambda)]^{1/2}](/2012-wikipedia_en_all_nopic_01_2012/I/4f775d6c3984a0da4c0b76e644342d92.png) . He analyzes the expansions of the cumulants of
. He analyzes the expansions of the cumulants of  up to the term
up to the term 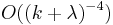 and shows that the following choices of
and shows that the following choices of  produce reasonable results:
produce reasonable results:
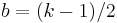 makes the second cumulant of
makes the second cumulant of  approximately independent of
approximately independent of 
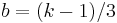 makes the third cumulant of
makes the third cumulant of  approximately independent of
approximately independent of 
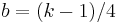 makes the fourth cumulant of
makes the fourth cumulant of  approximately independent of
approximately independent of 
Also, a simpler transformation 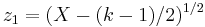 can be used as a variance stabilizing transformation that produces a random variable with mean
can be used as a variance stabilizing transformation that produces a random variable with mean 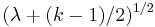 and variance
and variance 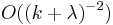 .
.
Usability of these transformations may be hampered by the need to take the square roots of negative numbers.
| Name | Statistic |
|---|---|
| chi-squared distribution | 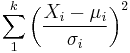 |
| noncentral chi-squared distribution | 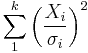 |
| chi distribution | 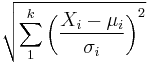 |
| noncentral chi distribution | 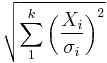 |
Notes
- ^ Muirhead (2005) Theorem 1.3.4
- ^ Nuttall, Albert H. (1975): Some Integrals Involving the QM Function, IEEE Transactions on Information Theory, 21(1), 95-96, ISSN 0018-9448
- ^ Sankaran , M. (1963). Approximations to the non-central chi-squared distribution Biometrika, 50(1-2), 199–204
- ^ Sankaran , M. (1959). "On the non-central chi-squared distribution", Biometrika 46, 235–237
- ^ Johnson et al. (1995) Section 29.8
- ^ Muirhead (2005) pages 22–24 and problem 1.18.
References
- Abramowitz, M. and Stegun, I.A. (1972), Handbook of Mathematical Functions, Dover. Section 26.4.25.
- Johnson, N. L., Kotz, S., Balakrishnan, N. (1970), Continuous Univariate Distributions, Volume 2, Wiley. ISBN 0-471-58494-0
- Muirhead, R. (2005) Aspects of Multivariate Statistical Theory, Wiley
- Siegel, A.F. (1979), "The noncentral chi-squared distribution with zero degrees of freedom and testing for uniformity", Biometrika, 66, 381–386
- Press, S.J. (1966), "Linear combinations of non-central chi-squared variates", The Annals of Mathematical Statistics 37 (2): 480–487, JSTOR 2238621
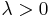 non-centrality parameter
non-centrality parameter